📃 Solution for Exercise M6.03#
The aim of this exercise is to:
verifying if a random forest or a gradient-boosting decision tree overfit if the number of estimators is not properly chosen;
use the early-stopping strategy to avoid adding unnecessary trees, to get the best generalization performances.
We use the California housing dataset to conduct our experiments.
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
data, target = fetch_california_housing(return_X_y=True, as_frame=True)
target *= 100 # rescale the target in k$
data_train, data_test, target_train, target_test = train_test_split(
data, target, random_state=0, test_size=0.5
)
Note
If you want a deeper overview regarding this dataset, you can refer to the Appendix - Datasets description section at the end of this MOOC.
Create a gradient boosting decision tree with max_depth=5 and
learning_rate=0.5.
# solution
from sklearn.ensemble import GradientBoostingRegressor
gbdt = GradientBoostingRegressor(max_depth=5, learning_rate=0.5)
Also create a random forest with fully grown trees by setting max_depth=None.
# solution
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(max_depth=None)
For both the gradient-boosting and random forest models, create a validation
curve using the training set to assess the impact of the number of trees on
the performance of each model. Evaluate the list of parameters param_range = np.array([1, 2, 5, 10, 20, 50, 100]) and use the mean absolute error.
# solution
import numpy as np
from sklearn.model_selection import ValidationCurveDisplay
param_range = np.array([1, 2, 5, 10, 20, 50, 100])
disp = ValidationCurveDisplay.from_estimator(
forest,
data,
target,
param_name="n_estimators",
param_range=param_range,
scoring="neg_mean_absolute_error",
negate_score=True,
std_display_style="errorbar",
n_jobs=2,
)
_ = disp.ax_.set(
xlabel="Number of trees in the forest",
ylabel="Mean absolute error (k$)",
title="Validation curve for random forest",
)
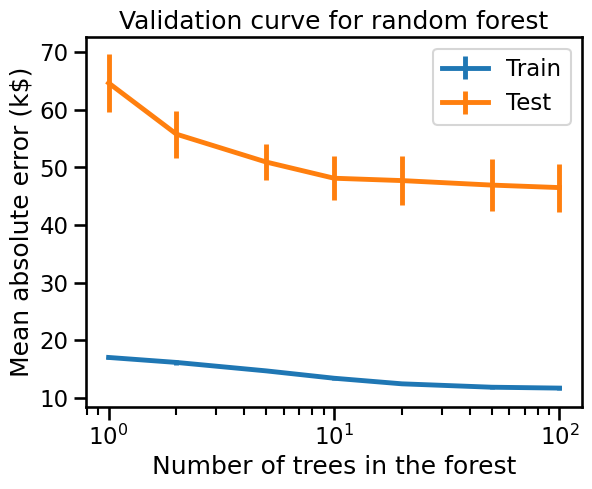
Random forest models improve when increasing the number of trees in the ensemble. However, the scores reach a plateau where adding new trees just makes fitting and scoring slower.
Gradient boosting models overfit when the number of trees is too large. To avoid adding a new unnecessary tree, unlike random-forest gradient-boosting offers an early-stopping option. Internally, the algorithm uses an out-of-sample set to compute the generalization performance of the model at each addition of a tree. Thus, if the generalization performance is not improving for several iterations, it stops adding trees.
Now, create a gradient-boosting model with n_estimators=1_000. This number
of trees is certainly too large. Change the parameter n_iter_no_change
such that the gradient boosting fitting stops after adding 5 trees to avoid
deterioration of the overall generalization performance.
# solution
gbdt = GradientBoostingRegressor(n_estimators=1_000, n_iter_no_change=5)
gbdt.fit(data_train, target_train)
gbdt.n_estimators_
294
We see that the number of trees used is far below 1000 with the current dataset. Training the gradient boosting model with the entire 1000 trees would have been detrimental.
Estimate the generalization performance of this model again using the
sklearn.metrics.mean_absolute_error metric but this time using the test set
that we held out at the beginning of the notebook. Compare the resulting value
with the values observed in the validation curve.
# solution
from sklearn.metrics import mean_absolute_error
error = mean_absolute_error(target_test, gbdt.predict(data_test))
print(f"On average, our GBDT regressor makes an error of {error:.2f} k$")
On average, our GBDT regressor makes an error of 34.28 k$
We observe that the MAE value measure on the held out test set is close to the validation error measured to the right hand side of the validation curve. This is kind of reassuring, as it means that both the cross-validation procedure and the outer train-test split roughly agree as approximations of the true generalization performance of the model. We can observe that the final evaluation of the test error seems to be even slightly below than the cross-validated test scores. This can be explained because the final model has been trained on the full training set while the cross-validation models have been trained on smaller subsets: in general the larger the number of training points, the lower the test error.

