Linear regression using scikit-learn#
In the previous notebook, we presented the parametrization of a linear model. During the exercise, you saw that varying parameters gives different models that may fit better or worse the data. To evaluate quantitatively this goodness of fit, you implemented a so-called metric.
When doing machine learning, one is interested in selecting the model which minimizes the error on the data available the most. From the previous exercise, we could implement a brute-force approach, varying the weights and intercept and select the model with the lowest error.
Hopefully, this problem of finding the best parameters values (i.e. that result in the lowest error) can be solved without the need to check every potential parameter combination. Indeed, this problem has a closed-form solution: the best parameter values can be found by solving an equation. This avoids the need for brute-force search. This strategy is implemented in scikit-learn.
import pandas as pd
penguins = pd.read_csv("../datasets/penguins_regression.csv")
feature_name = "Flipper Length (mm)"
target_name = "Body Mass (g)"
data, target = penguins[[feature_name]], penguins[target_name]
Note
If you want a deeper overview regarding this dataset, you can refer to the Appendix - Datasets description section at the end of this MOOC.
from sklearn.linear_model import LinearRegression
linear_regression = LinearRegression()
linear_regression.fit(data, target)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression()
The instance linear_regression stores the parameter values in the attributes
coef_ and intercept_. We can check what the optimal model found is:
weight_flipper_length = linear_regression.coef_[0]
weight_flipper_length
np.float64(49.68556640610011)
intercept_body_mass = linear_regression.intercept_
intercept_body_mass
np.float64(-5780.831358077066)
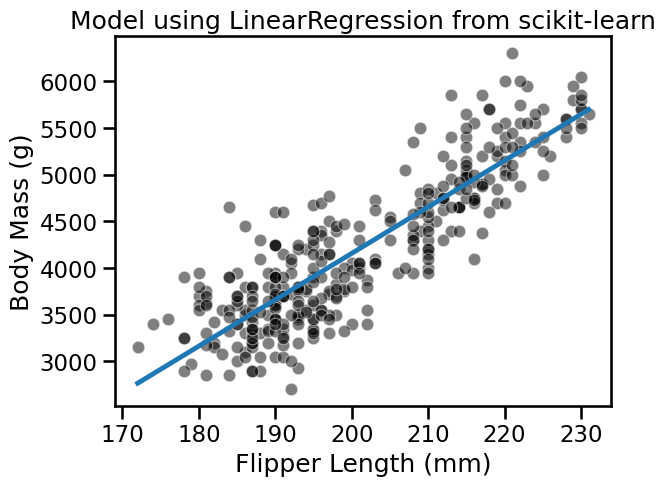
We can use the weight and intercept to plot the model found using the scikit-learn.
import numpy as np
flipper_length_range = np.linspace(data.min(), data.max(), num=300)
predicted_body_mass = (
weight_flipper_length * flipper_length_range + intercept_body_mass
)
import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(x=data[feature_name], y=target, color="black", alpha=0.5)
plt.plot(flipper_length_range, predicted_body_mass)
_ = plt.title("Model using LinearRegression from scikit-learn")
In the solution of the previous exercise, we implemented a function to compute the goodness of fit of a model. Indeed, we mentioned two metrics: (i) the mean squared error and (ii) the mean absolute error. Let’s see how to use the implementations from scikit-learn in the following.
We can first compute the mean squared error.
from sklearn.metrics import mean_squared_error
inferred_body_mass = linear_regression.predict(data)
model_error = mean_squared_error(target, inferred_body_mass)
print(f"The mean squared error of the optimal model is {model_error:.2f}")
The mean squared error of the optimal model is 154546.19
A linear regression model minimizes the mean squared error on the training
set. This means that the parameters obtained after the fit (i.e. coef_ and
intercept_) are the optimal parameters that minimizes the mean squared
error. In other words, any other choice of parameters would yield a model with
a higher mean squared error on the training set.
However, the mean squared error is difficult to interpret. The mean absolute error is more intuitive since it provides an error in the same unit as the one of the target.
from sklearn.metrics import mean_absolute_error
model_error = mean_absolute_error(target, inferred_body_mass)
print(f"The mean absolute error of the optimal model is {model_error:.2f} g")
The mean absolute error of the optimal model is 313.00 g
A mean absolute error of 313 means that in average, our model make an error of ± 313 grams when predicting the body mass of a penguin given its flipper length.
In this notebook, you saw how to train a linear regression model using scikit-learn.

